1235 Maximum Profit in Job Scheduling

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

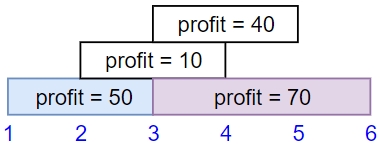
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

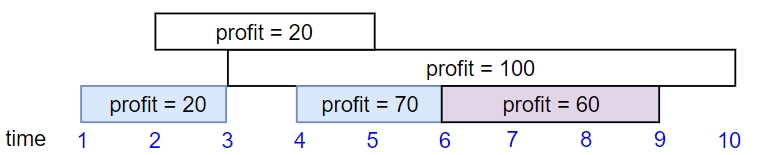
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 104

• 1 <= startTime[i] < endTime[i] <= 109

• 1 <= profit[i] <= 104

一开始看的时候，被图迷惑了，用了profit value做dp的长度。所以后面如果有重复的profit时，下标处理混乱，没做出来。然后看了solution里大神的做法。其实，感觉这个跟354 Russian Doll Envelope 很像！也是先排序，然后dp表示的是到i为止，能达到的最优值。这里转换方程其实是，max（i这段+前面的段s，不用i这段）-> max（i + dp[j], dp[i - 1])。

这题好像比300那个的二分简单。因为这里排序了，只要注意找的是最后一个 j.endTime <= i.startTime的就好了。T: O(N), S: O(N)

class Solution {
    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        if (startTime == null || startTime.length == 0 || 
            endTime == null || endTime.length == 0 || 
            profit == null || profit.length == 0) {
                return 0;
        }

        int len = startTime.length;
        Entry[] entries = new Entry[len];
        for (int i = 0; i < len; i++) {
            entries[i] = new Entry(startTime[i], endTime[i], profit[i]);
        }

        Arrays.sort(entries, (e1, e2) -> e1.end - e2.end);
        int[] dp = new int[len];
        dp[0] = entries[0].profit;
        for (int i = 1; i < len; i++) { 
            // 上来先比较一下自己的profit和之前的profit哪个大
            dp[i] = Math.max(dp[i - 1], entries[i].profit);
            
            int j = findLastInEntries(entries, 0, i - 1, entries[i].start);
            // 排在前面的那些entry可能没有end小于自己start的前面的段
            if (j == -1) { 
                continue;
            }
            // 比较的是，max（用i这段entry + 前面的段，不用i这段entry）
            dp[i] = Math.max(dp[i], entries[i].profit + dp[j]);
            // for (int j = i; j >= 0; j--) { // 不二分就直接loop一圈，n^2
            //     if (entries[j].end <= entries[i].start) {
            //         dp[i] = Math.max(dp[i], entries[i].profit + dp[j]);
            //         break;
            //     }
            // }

        }        
        return dp[len - 1];
    }

    private int findLastInEntries(Entry[] entries, int start, int end, int target) {
        while (start + 1 < end) {
            int mid = start + (end - start) / 2; 
            int curVal = entries[mid].end;
            if (curVal == target) {
                start = mid;
            } else if (curVal > target) {
                end = mid;
            } else {
                start = mid;
            }
        }

        if (entries[end].end <= target) {
            return end;
        }

        if (entries[start].end <= target) {
            return start;
        }

        return -1;
    }
}

class Entry {
    int start;
    int end;
    int profit;

    public Entry(int s, int e, int p) {
        start = s;
        end = e;
        profit = p;
    }
}