308 Range Sum Query 2D - Mutable

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

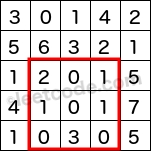The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10

Note:

1. The matrix is only modifiable by the update function.

2. You may assume the number of calls to update and sumRegion function is distributed evenly.

3. You may assume that row1 ≤ row2 and col1 ≤ col2.

嘛，就是二维的BIT，跟307 Range Sum Query - Mutable一样，因为要疯狂update，所以不能用304 Range Sum Query 2D 来算prefixsum。这里算法就是除了算i以外，j也加进来了。具体树长什么样，不知道。但估计操作也可以拓展到3维。

因为会off by one，所以updateBIT要分开写，因为创建的时候，不用+1，真正更新的时候要+1。

• Time Complexity

  • Update (2D) - O(logN⋅logM)

  • Query (2D) - O(logN⋅logM)

  • Build (2D) - O(N⋅M⋅logN⋅logM)

  • Here N denotes the number of rows and M denotes the number of columns.

• Space Complexity

  • O(NM) - Since we'll need an extra bit matrix to store the non-overlapping partial sums

int[][] BIT;
int n;
int m;
public NumMatrix(int[][] matrix) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
        return;
    }
    n = matrix.length;
    m = matrix[0].length;
    BIT = new int[n + 1][m + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            updateBIT(i, j, matrix[i - 1][j - 1]);
        }
    }
}

public void update(int row, int col, int val) {
    int oldVal = sumRegion(row, col, row, col);
    int diff = val - oldVal;

    updateBIT(row + 1, col + 1, diff);
}

public int sumRegion(int row1, int col1, int row2, int col2) {
    int toBottomRight = getPrefixSum(row2 + 1, col2 + 1);
    int toTopLeft = getPrefixSum(row1, col1);
    int toBottomLeft = getPrefixSum(row1, col2 + 1);
    int toTopRight = getPrefixSum(row2 + 1, col1);
    return toBottomRight + toTopLeft - toBottomLeft - toTopRight;
}

private int getPrefixSum(int row, int col) {
    int sum = 0;
    for (int i = row; i > 0; i -= lsb(i)) {
        for (int j = col; j > 0; j -= lsb(j)) {
            sum += BIT[i][j];                
        }
    }
    return sum;
}

private int lsb(int index) {
    return index & -index;
}

private void updateBIT(int row, int col, int val) {
    for (int i = row; i <= n; i += lsb(i)) {
        for (int j = col; j <= m; j += lsb(j)) {
            BIT[i][j] += val;                
        }
    }
}