785 Is Graph Bipartite

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).

• There are no parallel edges (graph[u] does not contain duplicate values).

• If v is in graph[u], then u is in graph[v] (the graph is undirected).

• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1: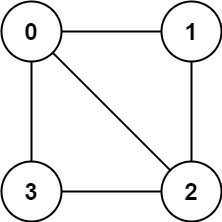

Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2: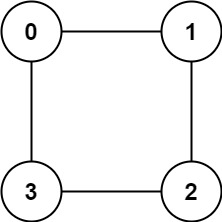

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

• graph.length == n

• 1 <= n <= 100

• 0 <= graph[u].length < n

• 0 <= graph[u][i] <= n - 1

• graph[u] does not contain u.

• All the values of graph[u] are unique.

• If graph[u] contains v, then graph[v] contains u.

如题，解法，bfs，用两种颜色填图里的点，规则是邻居跟自己要是填不同颜色。如果填着填着发现颜色相同的话，返回false。这题在geeksforgeeks上有oj，不过是用邻接表的。其实填色还能用这个color[nei] = color[node] ^ 1; solution是用stack做的，可以参考参考。其实就是把图里的点和边都过一遍，所以T:O(n + e), S:O(n)

// n年后再写
public boolean isBipartite(int[][] graph) {
    if (graph == null) {
        return false;
    }
    
    int n = graph.length;
    int[] colored = new int[n];
    
    boolean bipartite = true;
    for (int i = 0; i < n; i++) {
        if (colored[i] == 0) {
            bipartite = bipartite & fillColor(i, graph, colored);
        }
    }
    
    return bipartite;
}

private boolean fillColor(int curNode, int[][] graph, int[] colored) {
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(curNode);
    colored[curNode] = 1;
    
    while (!queue.isEmpty()) {
        int node = queue.poll();
        int[] neighbor = graph[node];
        for (int nei : neighbor) {
            if (colored[nei] == 0) {
                queue.offer(nei);
                colored[nei] = 0 - colored[node];
            } else {
                if (colored[nei] == colored[node]) {
                    return false;
                }
            }
        }
    }
    
    return true;
}

/*Complete the function below*/
class GfG {
    static int[] colored;
    public static boolean isBipartite(int G[][],int src,int V)    {
        if (G == null || G.length == 0 || G[0].length == 0) {
            return false;
        }

        colored = new int[V];
        Arrays.fill(colored, -1);

        for (int v = 0; v < V; v++) {//因为图可能不联通，这里多加一层，把图全遍历完
            if (colored[v] == -1) {
                if (!fillColor(src, G, V)) {
                    return false;
                }
            }
        }

        return true;
    }

    private static boolean fillColor(int src, int G[][], int V) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(src);
        colored[src] = 1;

        while (!queue.isEmpty()) {
            int node = queue.poll();

            for (int v = 0; v < V; v++) {
                if (G[node][v] == 1) {
                    if (colored[v] == -1) {
                        colored[v] = 1 - colored[node];
                        queue.offer(v);
                    } else {
                        if (colored[v] == colored[node]) {
                            return false;
                        }
                    }
                }
            }
        }

        return true;
    }
}

// 参考答案
public boolean isBipartite(int[][] graph) {
    int n = graph.length;
    int[] color = new int[n];
    Arrays.fill(color, -1);

    for (int start = 0; start < n; ++start) {
        if (color[start] == -1) {
            Stack<Integer> stack = new Stack();
            stack.push(start);
            color[start] = 0;

            while (!stack.empty()) {
                Integer node = stack.pop();
                for (int nei: graph[node]) {
                    if (color[nei] == -1) {
                        stack.push(nei);
                        color[nei] = color[node] ^ 1;
                    } else if (color[nei] == color[node]) {
                        return false;
                    }
                }
            }
        }
    }

    return true;
}