1437 Check If All 1's Are at Least Length K Places Away

Given an array nums of 0s and 1s and an integer k, return True if all 1's are at least k places away from each other, otherwise return False.

Example 1:

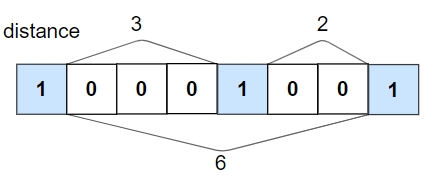
Input: nums = [1,0,0,0,1,0,0,1], k = 2
Output: true
Explanation: Each of the 1s are at least 2 places away from each other.

Example 2:

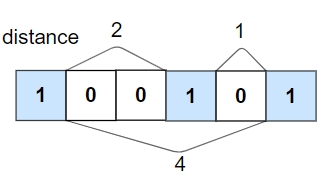
Input: nums = [1,0,0,1,0,1], k = 2
Output: false
Explanation: The second 1 and third 1 are only one apart from each other.

Example 3:

Input: nums = [1,1,1,1,1], k = 0
Output: true

Example 4:

Input: nums = [0,1,0,1], k = 1
Output: true

Constraints:

• 1 <= nums.length <= 105

• 0 <= k <= nums.length

• nums[i] is 0 or 1

一开始想到的是strstr那样的解法，还是调了一阵子才不off by one。T: O(n)

public boolean kLengthApart(int[] nums, int k) {
    if (nums == null || nums.length == 0 || k < 0) {
        return false;
    }

    for (int i = 0; i < nums.length; i++) {
        if (nums[i] == 0) {
            continue;                
        }
        for (int j = 0; j < k && j + i + 1 < nums.length; j++) {
            if (nums[i + j + 1] == 1) {
                return false;
            }
        }
    }

    return true;
}

一看答案，发现自己傻了

public boolean kLengthApart(int[] nums, int k) {
    // initialize the counter of zeros to k
    // to pass the first 1 in nums
    int count = k;

    for (int num : nums) {
        // if the current integer is 1
        if (num == 1) {
            // check that number of zeros in-between 1s
            // is greater than or equal to k
            if (count < k) {
                return false;    
            }
            // reinitialize counter
            count = 0;

        // if the current integer is 0
        } else {
            // increase the counter
            ++count;    
        } 
    }        
    return true;
}

这题的一个变种是给你一个integer，让你判断它的二进制representation是否符合这个规则。那个得用bit manipulation来做，听说是前东家的题。这里把nums变integer来做模拟。

这个做法主要是从屁股开始，一边remove 0一边数数，数到有1的话，我们check一下是不是起码有k个，如果小于k的话，就return false。

public boolean kLengthApart(int[] nums, int k) {
    // convert binary array into int
    int x = 0;
    for (int num : nums) {
        x = (x << 1) | num;    
    }

    // base case
    if (x == 0 || k == 0) {
        return true;    
    }

    // remove trailing zeros
    while ((x & 1) == 0) {
        x = x >> 1;    
    }

    while (x != 1) {
        // remove trailing 1-bit
        x = x >> 1;

        // count trailing zeros
        int count = 0;
        while ((x & 1) == 0) {
            x = x >> 1;
            ++count;    
        }

        // number of zeros in-between 1-bits
        // should be greater than or equal to k
        if (count < k) {
            return false;    
        }    
    }
    return true;
}