1631 Path With Minimum Effort

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3: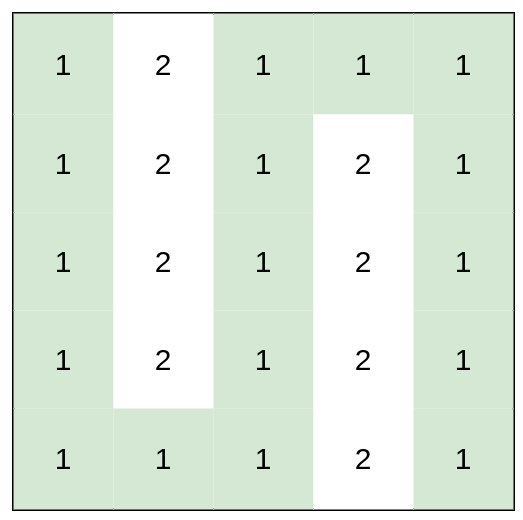

Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

• rows == heights.length

• columns == heights[i].length

• 1 <= rows, columns <= 100

• 1 <= heights[i][j] <= 10^6

一开始看题，各种纠结到底能不能不暴力搜，用DP。想了半天好像没有什么递推式。就算做也只能memo。但memo好像也不太行。所以只好看答案了。谁知，是一条二分答案。但其中用到BFS或者DFS。判断条件是，能不能用cost为mid，走完这图。因为最大的数值是10^6，所以6次能搜完range。（log（range））。然后，图的遍历，是O(V + E)。V是m*n，E也是m*n，所以T:O(m*n)。S：O(m*n)，visited的size

public int minimumEffortPath(int[][] heights) {
    if (heights == null || heights.length == 0 || heights[0].length == 0) {
        return Integer.MAX_VALUE;
    }

    int start = 0;
    int end = 1000000;

    while (start + 1 < end) {
        int mid = start + (end - start) / 2;
        if (canReach(mid, heights)) {
            end = mid;
        } else {
            start = mid;
        }
    }

    if (canReach(start, heights)) {
        return start;
    } else {
        return end;
    }
}

private boolean canReach(int cost, int[][] heights) {        
    int n = heights.length;
    int m = heights[0].length;

    boolean[][] visited = new boolean[n][m];

    int[] x = {0, 0, 1, -1};
    int[] y = {1, -1, 0, 0};

    Queue<Integer> queue = new LinkedList<>();

    queue.offer(0);
    visited[0][0] = true;

    while (!queue.isEmpty()) {
        int cur = queue.poll();
        int curi = cur / m;
        int curj = cur % m;

        for (int k = 0; k < 4; k++) {
            int nexti = curi + x[k];
            int nextj = curj + y[k];

            if (inBound(nexti, nextj, n, m) && !visited[nexti][nextj]) {
                if (Math.abs(heights[nexti][nextj] - heights[curi][curj]) <= cost) {
                    visited[nexti][nextj] = true;
                    queue.offer(nexti * m + nextj);
                    // 提前return，没有也不错，但有了快点
                    if (nexti == n - 1 && nextj == m - 1) {
                        return true;
                    }
                }
            }
        }

    }
    // 如果这里直接说false的话，那么只有一个点的图就不对了。所以要判断是否visit到了最后一个点
    return visited[n - 1][m - 1];
}

private boolean inBound(int row, int col, int n, int m) {
    if (row < 0 || col < 0 || row >= n || col >= m) {
        return false;
    }
    return true;
}